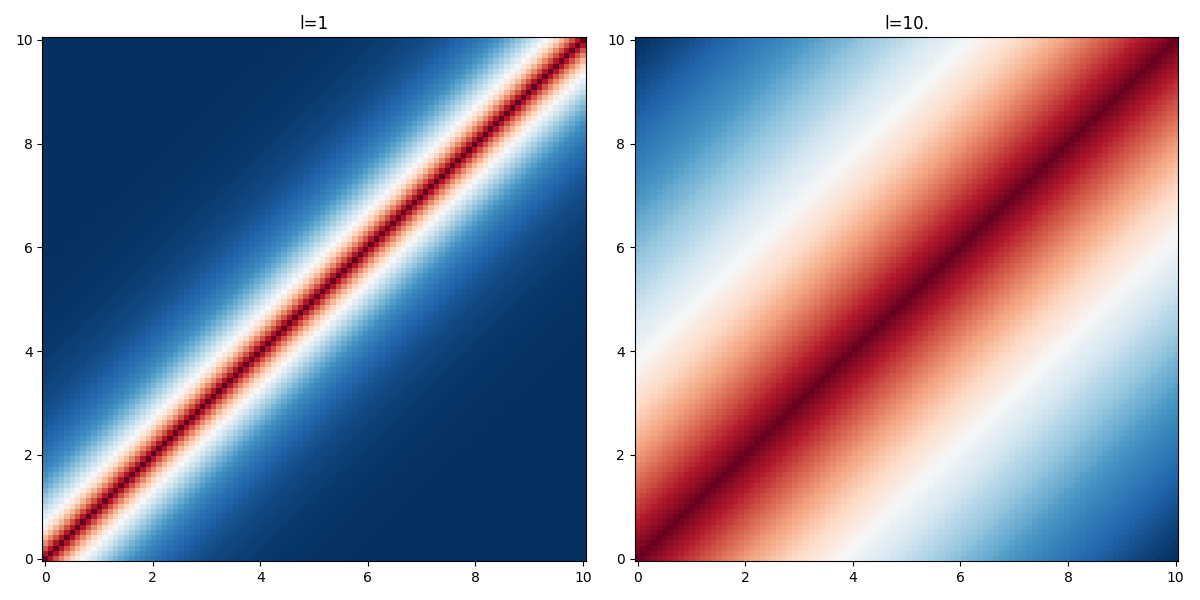
Ornstein-Uhlenbeck kernel
The Laplacian function kernel defines a stationary gaussian process, the Ornstein-Uhlenbeck process:
\begin{align*} \displaystyle K(x, x') &= \sigma^2\,\exp\left(-\frac{|d|}{l}\right),\quad d=x'-x \end{align*}
Unlike the Wiener process, this process is mean reverting and admits a stationary probability distribution. It is convenient to model time-series. It can be seen as a noisy relaxation model. ( p.212)
The parameter \(l\) is the characteristic lengthscale of the process. As one can see on the figure below, the larger the value of \(l\) the “further” the kernel takes non-negligible values.